感知机的原理及实现
条评论前言
经过第一章漫长的学习,终于进入到了算法的学习,也很激动地开始了对感知机的学习。
感知机模型
感知机的定义
假设输入空间(特征空间)是$\mathcal{X} \subseteq R^n$,输出空间是$\mathcal{Y}=\{+1,-1\}$,输入$x\in\mathcal{X}$表示实例的特征向量,对应于输入空间(特征空间)的点;输出$y\in\mathcal{Y}$表示实例的类别,由输入空间到输出空间的如下函数:
$$f(x)=sign(w\bullet x+b)$$
称为感知机,其中,w和b为感知机模型参数,$w\in R^n$叫作权值(weight)或权值向量(weight vector),$b\in R$叫作偏置(biss),$w\bullet x$表示w和x的内积,sign表示符号函数,即:
$$sign(x)=\begin{cases}
+1,x\ge 0 \\
-1,x<0\end{cases}$$
感知机是一种线性分类模型,属于判别模型。感知机模型的假设空间是定义在特征空间中的所有线性分类模型或线性分类器,即函数集合$ \{ f|f(x)=w\bullet x+b=0 \} $
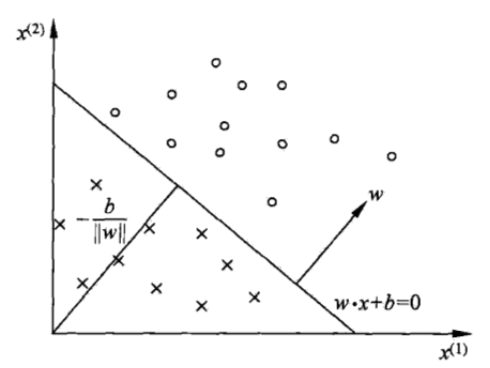
对于特征空间$R^n$中的一个超平面$S$,其中w是超平面的法向量,$b$是超平面的截距。这个超平面将特征空间划分为两个部分,位于两部分的点(特征向量)分别被分为正、负两类,因此超平面S被称为分离超平面。如下图所示:
感知机学习策略
数据集的线性可分性
定义(数据集的线性可分性):给定一个数据集$$T=\{(x_1,y_1),(x_2,y_2),…,(x_N,y_N)\}$$
其中$x_i\in \mathcal{X}=R^n$,$y_i\in \mathcal{Y}=\{+1,-1\}$,$i=1,2,…,N$,如果存在某个超平面$S$$$w\bullet x_i +b <0$$能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧,即对所有$y_i=+1$的实例$i$,有$w\bullet x_i+b>0$,对所有$y_i=1$的实例$i$,有$w\bullet x_i+b<0$,则称数据集T为线性可分数据集,否则称数据集T线性不可分。
在我的理解中,问题的关键在于存不存在一个超平面将所有的数据集按照正例负例分割开来,若存在,则线性可分;不存在,则线性不可分。
感知机学习策略
如果训练数据集是线性可分的,感知机学习的目标是找到能够将正、负实例点完全正确分开的分离超平面,为了找到这样的超平面,我们也就要找到感知机的参数,因此需要确定一个学习策略,即定义(经验)损失函数并将损失函数极小化。
损失函数的选择有很多,最简单的一个就是误分点的个数,但是这样的损失函数并不是参数w、b的连续可导函数,不容易优化。另一个选择则是误分类点到超平面S的总距离,这个是感知机所采用的。
输入空间$R^n$中任一点$x_0$到超平面S的距离:
$$\frac {1}{||w||} |w\bullet x_0+b|,其中||w||是w的L_2范数$$
其次,对于误分类的数据$(x_i,y_i)$,来说$$-y_i(w\bullet x_i+b)>0$$成立,也意味着预测得到值和真实值符号相反。
这样,假设超平面S的误分类点集合为M,那么所有误分类点到超平面S的总距离为:$$-\frac{1}{||w||} \sum_{x_i\in M}{y_i(w\bullet x_i+b)}$$不考虑$\frac{1}{||w||}$,就得到感知机学习的损失函数.
$$L(w,b)=-\sum_{x_i\in M}{y_i(w\bullet x_i+b)}$$
其中,$M$是误分类点的集合,这个损失函数就是感知机学习的经验风险函数。
可以看出,损失函数$L(w,b)$是非负的,如果没有误分类点,损失函数值是0.而误分类点越少,误分类点距离超平面也就越近,损失函数值就越小。一个特定的样本点的损失函数:在误分类时是参数$w,b$的线性函数,在正确分类时为0,因此在给定训练数据T,损失函数$L(w,b)$是$w,b$的连续可导函数。
感知机学习算法
感知机学习算法的原始形式
感知机算法其实就是求解损失函数极小化问题的解$$\min_{w,b} L(w,b)=-\sum_{x_i\in M} y_i(w\bullet x_i +b)$$
感知机学习算法是由误分类驱动的,具体采用随机梯度下降法,过程是首先,任意选取一个超平面$w_0,b_0$,然后用梯度下降法不断地极小化目标函数,一次随机选取一个误分类点使其梯度下降。
假设误分类点集合M是固定的,那么损失函数$L(w,b)$的梯度如下:
$$\nabla_w L(w,b)=-\sum_{x_i\in M} y_ix_i\\
\nabla_b L(w,b)=-\sum_{x_i\in M} y_i$$
随机选取一个误分类点$(x_i,y_i)$,对$w,b$进行更新:
$$w \gets w+\eta y_ix_i \\
b \gets b+\eta y_i$$
其中,式子中的$\eta$是步长,也就是我们熟知的学习率(learning rate)。
感知机学习算法的原始形式算法
输入:训练数据集$T={(x_1,y_1),(x_2,y_2),…,(x_N,y_N)}$,其中$x_i \in \mathcal{X} = R^n$,$y_i \in \mathcal{Y}=\{-1,+1\}$,$i=1,2,…,N$,学习率$\eta(0<\eta\le 1);$
输出:$w,b$,感知机模型$f(x)=sign(w\bullet x+b)$.
- 选取初值$w_0,b_0$
- 在训练集中选取数据$(x_i,y_i)$
- 如果$y_i(w\bullet x_i+b)\le 0$ $$w \gets w+\eta y_ix_i$$$$b \gets b+\eta y_i$$
- 转至2步骤,直至训练集中没有误分类点。
这种学习方法在直观上有如下解释:当一个实例点被误分类,即位于分离超平面的错误一侧时,则调整$w,b$的值,使分离超平面向该误分类点的一侧移动,以减少该误分类点与超平面间的距离,直至超平面越过该分类点使其被正确分类。
感知机学习算法的原始形式的实现
code
根据上述的原始形式算法,直接构建算法模型,数据是通过公式创造的,然后用于分类,实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77import random
import numpy as np
from matplotlib import pyplot as plt
# 创建数据集
def createData(t_w,t_b,num_size):
random.seed(78)
x,y=[],[]
for i in range(num_size):
x.append([random.uniform(0,10),random.uniform(0,10)])
for i in x:
sy=i[0]*t_w[0]+i[1]*t_w[1]
if sy>t_b:
y.append(1)
else:
y.append(-1)
x=np.array(x)
y=np.array(y)
return x,y
#训练过程
def train(x,y,learning_rate):
w=np.array([0,0])
b=0
finish_flag=False
num=0
while(not finish_flag):
num+=1
finish_flag=True
f_num=0
for i in range(len(y)):
if y[i]*(np.dot(w,x[i])+b)<=0:
w=w+learning_rate*y[i]*x[i]
b=b+learning_rate*y[i]
finish_flag=False
f_num+=1
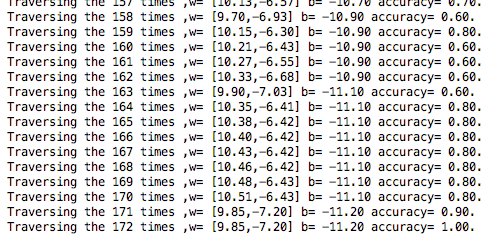
print("Traversing the {} times ,w= [{:.2f},{:.2f}] b= {:.2f} accuracy= {:.2f}.".format(num,w[0],w[1],b,(10-f_num)/10))
return w,b
#预测出来的model
def f(w,b):
x1 = np.arange(0, 10, 0.1)
return x1,[-(w[0]*i+b)/w[1] for i in x1]
#图像展示
def show(x,y,w,b):
x1=np.dot(x,[1,0])
x2=np.dot(x,[0,1])
color=[]
for i in np.array([i==-1 for i in y]):
if i:
color.append(255)
else:
color.append(0)
plt.scatter(x1,x2,c=color)
xx,yy=f(w,b)
plt.plot(xx,yy)
plt.xlabel("x0")
plt.ylabel("x1")
plt.xlim(0,10)
plt.ylim(0,10)
plt.title("Realization of perceptron")
plt.show()
if __name__ == '__main__':
t_w=np.array([3,-2]) #学习方便,仅设计两个参数,两个特征值
t_b=4.3 #生成值的b
num_size=80 #创造的训练数据量
learning_rate=0.1
x,y=createData(t_w,t_b,num_size)
print("*"*10,"train data","*"*10)
for i in range(10):
print("{}*w0+{}*w1+b >= 0? {}".format(x[i][0],x[i][1],y[i]))
print("*"*10,"Answer","*"*10)
w,b=train(x,y,learning_rate)
show(x,y,w,b)
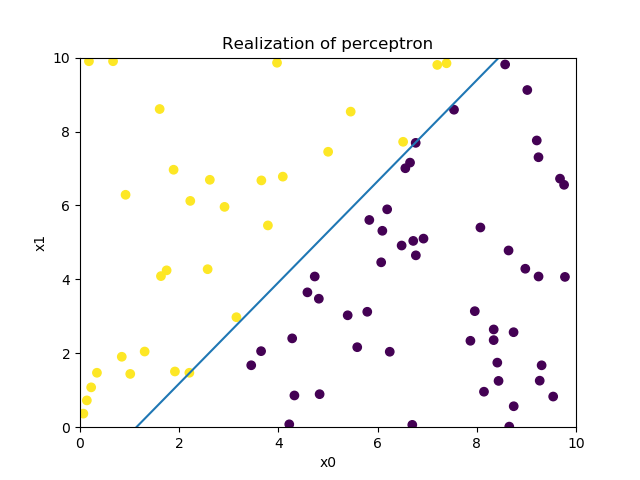
实现结果
感知机学习算法的对偶形式
输入:线性可分的数据集$T={(x_1,y_1),(x_2,y_2),…,(x_N,y_N)}$,其中$x_i \in R^n$,$x_i \in R^n,y_i \in \{-1,+1\},i=1,2,…,N$,$学习率\eta(0<\eta\le 1)$
输出:$\alpha,b$;感知机模型$f(x)=sign(\sum_{j=1}^{N}\alpha_j y_j x_j+b)$,其中$\alpha = (\alpha_1,\alpha_2,…,\alpha_N)^T.$
- $\alpha\gets 0,b\gets 0$
- 在训练集中选取数据$(x_i,y_i)$
- 如果$y_i\lgroup\sum_{j=1} ^N{\alpha_j y_j x_i +b}\rgroup\le 0$ $$\alpha_i \gets \alpha_i+\eta$$ $$b\gets b+\eta y_i$$
- 转至2直到没有误分类数据
对偶形式中训练实例仅为内积的形式出现,为了方便,可以预先将训练集中实例的内积计算出来并用矩阵的形式存储,这个矩阵就是所谓的Gram矩阵$$G=[x_i\bullet x_j]_{N\times N}$$
感知机学习算法的对偶形式的实现
code
与原始形式不同的地方在于实例中的内积是通过求解Gram矩阵获得,详细代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104# -*- coding: utf-8 -*-
# @Author : yechenchen
# @Time : 2018/10/9 下午5:19
# @File : 感知机学习算法的对偶形式.py
# @Software : PyCharm Community Edition
#感知机学习算法的对偶形式,P33
import numpy as np
from matplotlib import pyplot as plt
np.random.seed(33)
#创建数据
def CreateData(h_size,w_size):
x=np.random.rand(h_size,w_size)
return (x)
#给予对应的真实值
def getY(X,feature_num):
w=np.random.rand(feature_num)
b=-0.2
print(w,b)
Y=np.array([])
for i in X:
if np.dot(w,i)+b>0:
Y=np.append(Y,[1])
else:
Y=np.append(Y,[-1])
return Y
#构建Gram矩阵
def getG(X):
G=np.zeros((len(X),len(X)))
for i in range(len(X)):
for t in range(len(X)):
G[i][t]=np.dot(X[i],X[t])
return G
#训练过程,默认学习率为0.1
def train(X,Y,G,feature_num,learning_rate=0.1):
a=np.zeros(len(Y))
b=0
finish_flag=False
num=0
while not finish_flag:
finish_flag=True
num+=1
f_num=0
for i in range(len(G)):
tmp=0
for j in range(len(Y)):
tmp+=(a[j]*Y[j]*G[i][j])
ans=Y[i]*(tmp+b)
if ans<=0:
a[i]+=1*learning_rate #更新a值
b+=Y[i]*learning_rate #更新b值
finish_flag=False
f_num+=1
print("Traversing the {} times , b= {:.2f} accuracy= {:.2f}.".format(num,b,(len(Y)-f_num)/len(Y)))
w=np.zeros(feature_num)
for i in range(len(X)):
w+=a[i]*X[i]*Y[i]
return w,b
#构建预测到的函数
def f(w,b):
x0 = np.arange(0, 10, 0.1)
return x0,[-(w[0]*i+b)/w[1] for i in x0]
#可视化显示得到的函数以及散点
def show(x,y,w,b):
x1=np.dot(x,[1,0])
x2=np.dot(x,[0,1])
color=[]
for i in np.array([i==-1 for i in y]):
if i:
color.append(255)
else:
color.append(0)
plt.scatter(x1,x2,c=color)
xx,yy=f(w,b)
plt.plot(xx,yy)
plt.xlabel("x0")
plt.ylabel("x1")
plt.xlim(0,1)
plt.ylim(0,1)
plt.title("Realization of perceptron")
plt.show()
#主函数
if __name__ == '__main__':
feature_num=2 #每个样本具备的特征值的数量,设为2时可以可视化输出,否则需要用PCA降维
data_size=80 #训练数据量
X=CreateData(data_size,feature_num) #每组数据五个特征值,共80组数据
Y=getY(X,feature_num)
print("*"*10,"train data","*"*10)
for i in range(data_size):
print(X[i],Y[i])
print("*" * 10, "train", "*" * 10)
G=getG(X)
w,b=train(X,Y,G,feature_num)
print("*" * 10, "ans", "*" * 10)
print("w={},b={}".format(w,b))
show(X,Y,w,b)
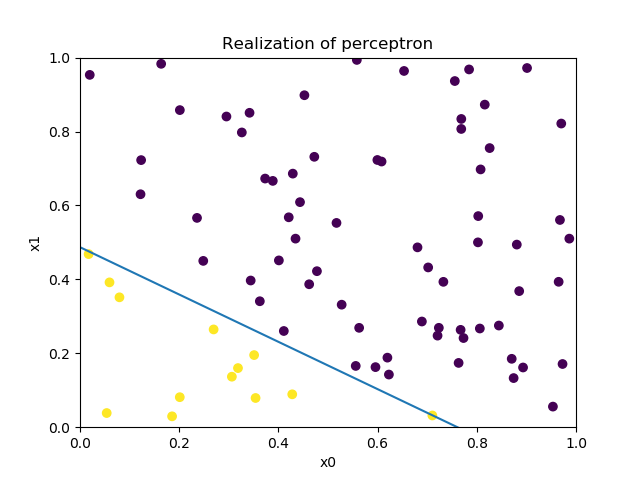
实现结果
- 本文链接:https://netycc.com/2018/10/10/感知机的原理及实现/
- 版权声明:本博客所有文章除特别声明外,均采用 CC BY-NC-SA 3.0 CN 许可协议。转载请注明出处!
分享