前言 在学习并实现完了之前的感知机算法,感觉它是比较简单的,并且只能进行处理线性分类问题。
k近邻算法 通俗的说:给定一个数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的k个实例,这k个实例的多数属于某个类,就把该输入实例分为这个类(多数表决投票)。
输入:训练数据集$T=\{(x_1,y_1),(x_1,y_2),…,(x_N,y_N)\}$其中,$x_i\in \mathcal{X}\subseteq R^n$为实例的特征向量,$y_i\in \mathcal{Y}={c_1,c_2,…,c_k}$为实例的类别,$i=1,2,…,N$;实例特征向量$x$;
当k近邻法的k=1时,就是特殊情形,也就是最近邻算法,对于输入的实例点(特征向量)$x$,最近邻法将训练数据集中与$x$最邻近点的类作为$x$的类。k近邻算法没有显式的学习过程。
距离度量 如《统计学习方法》概论总结中所说,距离的度量方法有很多,特征空间中两个实例点的距离是两个实例点相似程度的反映。k近邻模型的特征空间一般是$n$维实数向量空间$R^n$。使用的距离是欧氏距离,但也可以是其他距离,如更一般的$L_p$距离或Minkowski距离。这里就不再赘述了。
k值的选择 k值的选择会对k近邻法的结果产生重大影响。
如果选择较小的k值,就相当于用较小的邻域中的训练实例进行预测,“学习”的近似误差会减小,只有于输入实例相近的训练实例才会对预测结果起作用。但是缺点是“学习”的估计误差会增大,预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声,预测就会出错。换句话说,k值的减小就意味着整体模型变得复杂,容易发生过拟合。
如果选择较大的k值,就相当于用较大领域中的训练实例进行预测。其优点是可以减少学习的估计误差。但缺点是学习的近似误差会增大。这时与输入实例较远的训练实例也会对预测起作用,使预测发生错误。k值的增大就意味着整体的模型变得简单。
在应用中,k值一般选择一个比较小的数值。通常采用交叉验证法来选取最优的k值。
分类决策规则 k近邻法中的分类决策规则往往是多数表决,即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类。
KNN的实现 code 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 import numpy as npfrom sklearn.datasets import load_irisfrom sklearn import preprocessingfrom sklearn.model_selection import train_test_splitnp.random.seed(33 ) def getIrisData () : data=load_iris() X=np.array(data.data) Y=np.array(data.target) min_max_scaler = preprocessing.MinMaxScaler() X = min_max_scaler.fit_transform(X) X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.2 , random_state = 33 ) return X_train, X_test, y_train, y_test class cell () : def __init__ (self,x,y) : self.x=x self.y=y class KNN () : def __init__ (self,k=11 ) : self.k=k def train (self,X,Y) : self.size=len(X[0 ]) self.cells=[] for i in range(len(Y)): self.cells.append(cell(X[i],Y[i])) def predict (self,x) : Nk=sorted(self.cells,key=lambda cell:np.linalg.norm(cell.x-x))[:self.k] ans=np.zeros(4 ,float) for i in Nk: ans[i.y]+=1 ans=ans/self.k return ans.argmax(),ans if __name__ == '__main__' : X_train, X_test, y_train, y_test=getIrisData() knn=KNN() knn.train(X_train,y_train) print("*" * 10 , "预测" , "*" * 10 ) t_num=0 for i in range(len(y_test)): p_y,ans=knn.predict(X_test[i]) if p_y==y_test[i]: t_num+=1 print("各参数:" ,X_test[i],"真实类:" ,y_test[i],"预测类:" ,p_y,"是否正确:" ,p_y==y_test[i],"置信度:" ,ans) print("*" * 10 , "结果" , "*" * 10 ) print("iris数据集中,交叉验证正确率:{:2f}" .format(t_num/len(y_test)))
结果
kd树寻找最邻近算法 构造算法
构造平衡kd树算法:
搜索算法
用kd树的最邻近 搜索:
(a)如果该结点保存的实例点比当前最近点距离目标点更近,则以该实例点为“当前最近点”
(4)当回退到根结点时,搜索结束,最后的“当前最近点”即为x的最邻近点。
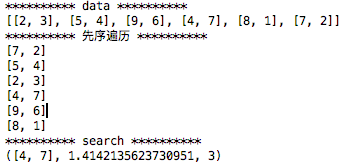
kd树查找最近邻的实现 code 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 import numpy as npclass KDnode () : def __init__ (self,dome_point,split_num,left,right) : self.dome_point=dome_point self.split_num=split_num self.left=left self.right=right class KDtree () : def __init__ (self,data) : k=len(data[0 ]) def CreateNode (split_num,data_set) : if not data_set : return None data_set.sort(key=lambda x : x[split_num]) split_pos=len(data_set)//2 middle_pos=data_set[split_pos] split_next=(split_num+1 )%k return KDnode(middle_pos,split_num, CreateNode(split_next,data_set[:split_pos]), CreateNode(split_next,data_set[split_pos+1 :])) self.root=CreateNode(0 ,data) def search (tree, point) : k = len(point) def travel (kd_node, target, max_dist) : if kd_node is None : return [0 ] * k, float("inf" ), 0 nodes_visited = 1 s = kd_node.split_num pivot = kd_node.dome_point if target[s] <= pivot[s]: nearer_node = kd_node.left further_node = kd_node.right else : nearer_node = kd_node.right further_node = kd_node.left temp1 = travel(nearer_node, target, max_dist) nearest = temp1[0 ] dist = temp1[1 ] nodes_visited += temp1[2 ] if dist < max_dist: max_dist = dist temp_dist = abs(pivot[s] - target[s]) if max_dist < temp_dist: return nearest, dist, nodes_visited temp_dist=np.linalg.norm((np.array(pivot)-np.array(target))) if temp_dist < dist: nearest = pivot dist = temp_dist max_dist = dist temp2 = travel(further_node, target, max_dist) nodes_visited += temp2[2 ] if temp2[1 ] < dist: nearest = temp2[0 ] dist = temp2[1 ] return nearest, dist, nodes_visited return travel(tree.root, point, float("inf" )) def preorder (root) : print(root.dome_point) if root.left: preorder(root.left) if root.right: preorder(root.right) if __name__ == '__main__' : data=[[2 ,3 ],[5 ,4 ],[9 ,6 ],[4 ,7 ],[8 ,1 ],[7 ,2 ]] print("*" *10 ,"data" ,"*" *10 ) print(data) kd=KDtree(data) print("*" *10 ,"先序遍历" ,"*" *10 ) preorder(kd.root) print("*" *10 ,"search" ,"*" *10 ) print(search(kd,[5 ,6 ]))
结果