前言

最近开始看自然语言处理的实战部分，看到了统计分词那里，统计分词用的模型是隐马尔可夫模型(HMM)，这里先介绍一下这个模型，它是可用于标注问题的统计学模型，描述由隐藏的马尔可夫链随机生成观测序列的过程，属于生成模型。

隐马尔可夫模型的基本概念

隐马尔可夫模型的定义

定义10.1(隐马尔可夫模型)
隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状态的序列，称为状态序列；每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列。序列的每一个位置又可以看作是一个时刻。

隐马尔可夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。隐马尔可夫模型的形式定义如下：
设$Q$是所有可能的状态的集合，$V$是所有可能的观测的集合。$$Q=\{q_1,q_2,…,q_N\}，V=\{v_1,v_2,…,v_M\}$$其中，$N$是可能的状态数，$M$是可能的观测数.以下$I$是长度为$T$的状态序列，$O$是对应的观测序列。$$I=(i_1,i_2,…,i_T)，O=(o_1,o_2,…,o_T)$$$A$是状态转移概率矩阵.$$A=[a_{ij}]_{N\times N}\tag{10.1}$$

其中，$$a_{ij}=P(i_{t+1}=q_j|i_t=q_i)，i=1,2,…,N;j=1,2,…,N\tag{10.2}$$是在时刻t处于$q_i$的条件下在时刻$t+1$转移到状态$q_j$的概率。
$B$是观测概率矩阵：$$B=[b_j(k)]_{N\times M}\tag{10.3}$$其中，$$b_j(k)=P(o_t=v_k|i_t=q_j)，k=1,2,…,M;j=1,2,…,N\tag{10.4}$$是在时刻$t$处于状态$q_j$的条件下生成观测$v_k$的概率。
$\pi$是初始状态概率向量：$$\pi=(\pi_i)\tag{10.5}$$其中，$$\pi_i=P(i_1=q_i)，i=1,2,…,N\tag{10.6}$$是时刻$t=1$处于状态$q_i$的概率。
隐马尔可夫模型由初始状态概率向量$\pi$、状态转移概率矩阵$A$和观测概率矩阵$B$决定。$\pi$和$A$决定状态序列，$B$决定观测序列。因此，隐马尔可夫模型$\lambda$可以用三元符号表示，即$$\lambda=(A,B,\pi)\tag{10.7}$$
$A,B,\pi$称为隐马尔可夫模型的三要素。
状态转移概率矩阵$A$与初始状态概率向量$\pi$确定了隐藏的马尔可夫链，生成不可观测的状态序列。观测概率矩阵$B$确定了如何从状态生成观测，与状态序列综合确定了如何产生观测序列。
从定义上可知，隐马尔可夫模型作了两个基本假设：

  1. 齐次马尔可夫性假设，即假设隐藏的马尔可夫链在任意时刻$t$的状态只依赖于其前一时刻的状态，与其他时刻的状态及观测无关，也与时刻$t$无关。$$P(i_t|i_{t-1},o_{t-1},…,i_1,o_1)=P(i_t|i_{t-1})，t=1,2,…,T\tag{10.8}$$
  2. 观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测及状态无关。$$P(o_t|i_T,o_T,i_{T-1},o_{T-1},…,i_{t+1},o_{t+1},i_t,i_{t-1},o_{t-1},…,i_1,o_1)=P(o_t|i_t)\tag{10.9}$$

  隐马尔可夫模型可以用于标注，这时状态对应着标记。标注问题是给定观测的序列预测其对应的标记序列。可以假设标注问题的数据是由隐马尔可夫模型生成的。这样我们可以利用隐马尔可夫模型的学习与预测算法进行标注。

观测序列的生成过程

  根据隐马尔可夫模型定义，可以将一个长度为$T$的观测序列$O=(O_1,O_2,…,O_T)$的生成过程描述如下：

算法10.1（观测序列的生成）
输入：隐马尔可夫模型$\lambda=(A,B,\pi)$，观测序列长度为$T$；
输出：观测序列$O=(o_1,o_2,…,o_T)$
(1)按照初始状态分布$\pi$产生状态$i_1$
(2)令$t=1$
(3)按照状态$i_t$的观测概率分布$b_{i_t}(k)$生成$o_t$
(4)按照状态$i_t$的状态转移概率分布$\{a_{i_ti_{t+1}}\}$产生状态$i_t+1，i_t+1=1,2,…,N$
(5)令$t=t+1$；如果$t<T$，转步(3)；否则，终止。

隐马尔可夫模型的3个基本问题

隐马尔可夫模型有三个基本问题：

  1. 概率计算问题。给定模型$\lambda=(A,B,\pi)$和观测序列$O=(o_1,o_2,…,o_T)$，计算在模型$\lambda$下观测序列$O$出现的概率$P(O|\lambda)$.
  2. 学习问题。已知观测序列$O=(o_1,o_2,…,o_T)$，估计模型$\lambda=(A,B,\pi)$参数，使得在该模型下观测序列概率$P(O|\lambda)$最大。即用极大似然估计的方法估计参数。
  3. 预测问题。已知模型$\lambda=(A,B,\pi)$和观测序列$O=(o_1,o_2,…,o_T)$，求对给定观测序列条件概率$P(I|O)$最大的状态序列$I=(i_1,i_2,…,i_T)$。即给定观测序列，求最有可能的对应的状态序列。

概率计算方法

  在这一节中，介绍一下计算观测序列概率$P(O|\lambda)$的前向(forward)和后向(backward)算法。先介绍概念上可行但计算上不可行的直接计算法。

直接计算法

  给定模型$\lambda=(A,B,\pi)$和观测序列$O=(o_1,o_2,…,o_T)$，计算观测序列$O$出现的概率$P(O|\lambda)$。最直接的方法是按概率公式直接计算。通过列举所有可能的长度为$T$的状态序列$I=(i_1,i_2,…,i_T)$，求各个状态序列I与观测序列$O=(o_1,o_2,…,o_T)$的联合概率$P(O,I|\lambda)$，然后对所有可能的状态序列求和，得到$P(O|\lambda)$.
  状态序列$I=(i_1,i_2,…,i_T)$的概率是$$P(I|\lambda)=\pi_{i_1}a_{i_1i_2}a_{i_2i_3}…a_{i_{T-1}i_T}\tag{10.10}$$
  对固定的状态序列I=（i_1,i_2,…,i_T)，观测序列$O=(o_1,o_2,…,o_T)$的概率是$P(O|I,\lambda)=b_{i_1}(o_1)b_{i_2}(o_2)…b_{i_T}(o_T)\tag{10.11}$
  $O$和$I$同时出现的联合概率为$$P(O|I,\lambda)=P(I|\lambda)=\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)…a_{i_{T-1}i_T}b_{i_T}(O_T)\tag{10.12}$$
  然后，对所有可能的状态序列$I$求和，得到观测序列$O$的概率$P(O|\lambda)$，即$$
\begin{split}
P(O|\lambda)&=\sum_IP(O|I,\lambda)P(I|\lambda)\\
&=\sum_{i_1,i_2,…,i_T}{\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)…a_{i_{T-1}i_T}b_{i_T}(O_T)}
\end{split}\tag{10.13}
$$
  但是，利用公式(10.13)计算量很大，是$O(TN^T)$阶的，这种算法不可行。

前向算法

  首先定义前向概率

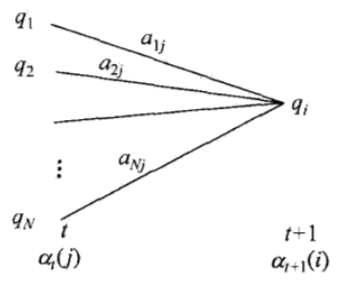
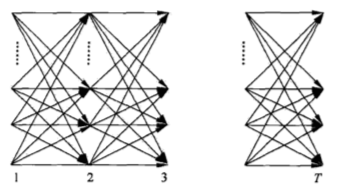
定义10.2（前向概率） 给定隐马尔可夫模型$\lambda$，定义到时刻$t$部分观测序列为$o_1,o_2,…,o_t$且状态为$q_i$的概率为前向概率，记作$$\alpha _t(i)=P(o_1,o_2,…,o_t,i_t=q_i|\lambda)\tag{10.14}$$

  可以递推地求得前向概率$\alpha_t(i)$及观测序列概率$P(O|\lambda)$。

算法10.2（观测序列概率的前向算法）
输入：隐马尔可夫模型$\lambda$，观测序列$O$;
输出：观测序列概率$P(O|\lambda)$.

  1. 初值$$\alpha_1(i)=\pi_ib_i(o_1),i=1,2,…,N\tag{10.15}$$
  2. 递推 对$t=1,2,…,T-1$.$$\alpha_{t+1}(i)=[\sum_{j=1}^{N}\alpha_t(j)a_{ji}]b_i(o_t+1),i=1,2,…,N\tag{10.16}$$
  3. 终止$$P(O|\lambda)=\sum_{i=1}^{N}\alpha_T(i)\tag{10.17}$$

图 10.1 前向概率的递推公式
图 10.2 观测序列路径结构

未完待续

HMM在统计分词中的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
class HMM(object):
    def __init__(self):
        import os

        # 主要是用于存取算法中间结果，不用每次都训练模型
        self.model_file = './data/hmm_model.pkl'

        # 状态值集合
        self.state_list = ['B', 'M', 'E', 'S']
        # 参数加载,用于判断是否需要重新加载model_file
        self.load_para = False

    # 用于加载已计算的中间结果，当需要重新训练时，需初始化清空结果
    def try_load_model(self, trained):
        if trained:
            import pickle
            with open(self.model_file, 'rb') as f:
                self.A_dic = pickle.load(f)
                self.B_dic = pickle.load(f)
                self.Pi_dic = pickle.load(f)
                self.load_para = True

        else:
            # 状态转移概率（状态->状态的条件概率）
            self.A_dic = {}
            # 发射概率（状态->词语的条件概率）
            self.B_dic = {}
            # 状态的初始概率
            self.Pi_dic = {}
            self.load_para = False

    # 计算转移概率、发射概率以及初始概率
    def train(self, path):

        # 重置几个概率矩阵
        self.try_load_model(False)

        # 统计状态出现次数，求p(o)
        Count_dic = {}

        # 初始化参数
        def init_parameters():
            for state in self.state_list:
                self.A_dic[state] = {s: 0.0 for s in self.state_list}
                self.Pi_dic[state] = 0.0
                self.B_dic[state] = {}

                Count_dic[state] = 0

        def makeLabel(text):
            out_text = []
            if len(text) == 1:
                out_text.append('S')
            else:
                out_text += ['B'] + ['M'] * (len(text) - 2) + ['E']

            return out_text

        init_parameters()
        line_num = -1
        # 观察者集合，主要是字以及标点等
        words = set()
        with open(path, encoding='utf8') as f:
            for line in f:
                line_num += 1

                line = line.strip()
                if not line:
                    continue

                word_list = [i for i in line if i != ' ']
                words |= set(word_list)  # 更新字的集合

                linelist = line.split()

                line_state = []
                for w in linelist:
                    line_state.extend(makeLabel(w))

                assert len(word_list) == len(line_state)

                for k, v in enumerate(line_state):
                    Count_dic[v] += 1
                    if k == 0:
                        self.Pi_dic[v] += 1  # 每个句子的第一个字的状态，用于计算初始状态概率
                    else:
                        self.A_dic[line_state[k - 1]][v] += 1  # 计算转移概率
                        self.B_dic[line_state[k]][word_list[k]] = \
                            self.B_dic[line_state[k]].get(word_list[k], 0) + 1.0  # 计算发射概率

        self.Pi_dic = {k: v * 1.0 / line_num for k, v in self.Pi_dic.items()}
        self.A_dic = {k: {k1: v1 / Count_dic[k] for k1, v1 in v.items()}
                      for k, v in self.A_dic.items()}
        # 加1平滑
        self.B_dic = {k: {k1: (v1 + 1) / Count_dic[k] for k1, v1 in v.items()}
                      for k, v in self.B_dic.items()}
        # 序列化
        import pickle
        with open(self.model_file, 'wb') as f:
            pickle.dump(self.A_dic, f)
            pickle.dump(self.B_dic, f)
            pickle.dump(self.Pi_dic, f)

        return self

    def viterbi(self, text, states, start_p, trans_p, emit_p):
        V = [{}]
        path = {}
        for y in states:
            V[0][y] = start_p[y] * emit_p[y].get(text[0], 0)
            path[y] = [y]
        for t in range(1, len(text)):
            V.append({})
            newpath = {}

            # 检验训练的发射概率矩阵中是否有该字
            neverSeen = text[t] not in emit_p['S'].keys() and \
                        text[t] not in emit_p['M'].keys() and \
                        text[t] not in emit_p['E'].keys() and \
                        text[t] not in emit_p['B'].keys()
            for y in states:
                emitP = emit_p[y].get(text[t], 0) if not neverSeen else 1.0  # 设置未知字单独成词
                (prob, state) = max(
                    [(V[t - 1][y0] * trans_p[y0].get(y, 0) *
                      emitP, y0)
                     for y0 in states if V[t - 1][y0] > 0])
                V[t][y] = prob
                newpath[y] = path[state] + [y]
            path = newpath

        if emit_p['M'].get(text[-1], 0) > emit_p['S'].get(text[-1], 0):
            (prob, state) = max([(V[len(text) - 1][y], y) for y in ('E', 'M')])
        else:
            (prob, state) = max([(V[len(text) - 1][y], y) for y in states])

        return (prob, path[state])

    def cut(self, text):
        import os
        if not self.load_para:
            self.try_load_model(os.path.exists(self.model_file))
        prob, pos_list = self.viterbi(text, self.state_list, self.Pi_dic, self.A_dic, self.B_dic)
        begin, next = 0, 0
        for i, char in enumerate(text):
            pos = pos_list[i]
            if pos == 'B':
                begin = i
            elif pos == 'E':
                yield text[begin: i + 1]
                next = i + 1
            elif pos == 'S':
                yield char
                next = i + 1
        if next < len(text):
            yield text[next:]

if __name__ == '__main__':
    hmm = HMM()
    hmm.train('./data/trainCorpus.txt_utf8')
    # hmm.try_load_model(True)
    text = '这是一个非常棒的方案！'
    while(text !='\n'):
        res = hmm.cut(text)
        print(text)
        print(str(list(res)))
        text=input()

分词结果